“五九卌五，四九卅六……”,日前在國家博物館開幕的秦簡文化展上，一片秦代的“九九表”木牘引起了大家的關注，古代的數(shù)學研究竟然如此超前。事實上，中國數(shù)學研究源遠流長，如今的十進位制計數(shù)法、勾股定理、圓周率等數(shù)學知識,早在千百年前就被古人們記錄和研究。今天，青年君就帶大家看看古人的數(shù)學成就，一起領略數(shù)千年前的中華智慧。

　　從原始社會萌芽的十進制算籌計數(shù)法

　　算籌計數(shù)法

　　十進，就是以十為基數(shù)，逢十進一位。十進制計數(shù)法在我國原始社會已開始萌芽，到奴隸社會初期的商代已發(fā)展成完整的十進制系統(tǒng)，并且有了“十”、“百”、“千”、“萬”等專用的大數(shù)名稱。

　　1899年，河南安陽發(fā)掘出大約3000多年前的殷代甲骨文，其中有一片甲骨上刻著“八日辛亥允戈伐二千六百五十六人”(八日辛亥那天的戰(zhàn)爭中消滅敵方2656人)。說明我國在公元前1600年，已經(jīng)采用了十進制計數(shù)法，早于第二使用者印度1000多年。

　　十進制計數(shù)法，是我們祖先對人類文明的一項不可磨滅的貢獻。馬克思在《數(shù)學手稿》中稱十進制計數(shù)法為“最妙的發(fā)明之一”，英國著名科技史學家李約瑟博士評價說：“如果沒有這種十進制，就幾乎不可能出現(xiàn)我們現(xiàn)在這個統(tǒng)一化的世界了。”

　　最早發(fā)現(xiàn)研究勾股定理的國家

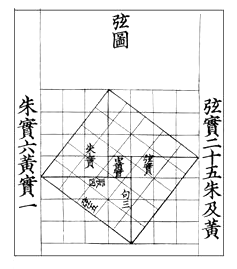
　　《勾股圓方圖說》注解圖

　　幾何學是數(shù)學中最古老且最基礎的分支之一。勾股定理則是幾何學中一顆光彩奪目的明珠，被稱作“幾何學的基石”。有些人以為勾股定理是外國數(shù)學家先研究發(fā)現(xiàn)的，但其實和十進制計數(shù)法一樣，我國是發(fā)現(xiàn)和研究勾股定理最早的國家。據(jù)《周髀算經(jīng)》記載：“故折矩以為勾廣三，股修四，徑隅五。”由于《周髀算經(jīng)》記錄的是公元前11世紀政治家周公與大夫商高的討論，所以它又被稱為商高定理。

　　三國時代的趙爽則在《周髀算經(jīng)注》里對勾股定理做出了詳細注釋。將勾股定理表述為：“勾股各自乘，并之，為弦實。開方除之，即弦。”證明方法敘述為：“按弦圖，又可以勾股相乘為朱實二，倍之為朱實四，以勾股之差自相乘為中黃實，加差實，亦成弦實。”他撰成《勾股圓方圖說》，附錄于《周髀》首章的注文中，用形數(shù)結合的方法，給出了勾股定理的詳細證明。

　　時至今日，初中數(shù)學教材的證明勾股定理的方法依舊采用的趙爽弦圖。

　　首創(chuàng)的“割圓術”與先進的圓周率研究

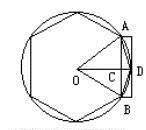
劉徽“割圓術”示意圖

　　“割圓術”是一種用圓內(nèi)接正多邊形的面積去無限逼近圓面積并以此求取圓周率的方法。這個方法是魏晉時期的數(shù)學家劉徽首創(chuàng)的。

　　“徑自相乘，三之，四而一”，是中國古代算數(shù)書所表述的圓的面積計算方法。意為圓的面積就是用圓的直徑的平方，乘以三，再除以四。由于古人并不知道圓周率，用這個方法計算出來的結果往往誤差很大。劉徽不滿足于這個結果，以極限思想為指導，提出用“割圓術”來求圓周率，并求得了3.14這個近似數(shù)值。自此之后，“割圓術”在圓周率計算史上被長期使用，作為最早的計算圓周率的方法一直為人們稱道。

　　劉徽之后約200年，大學者祖沖之進一步將圓內(nèi)接正多邊形邊數(shù)增加到24576，在計算了一萬多遍之后終于得出圓周率在3.1415926至3.1415927之間。他是世界上第一個把圓周率的數(shù)值算到小數(shù)點以后七位的人，此后約1000年中，這始終都是當時世界上最精確的圓周率數(shù)值。歐洲數(shù)學家奧托在一千多年以后，才算出了這個數(shù)值。

　　測量太陽高度的重差術

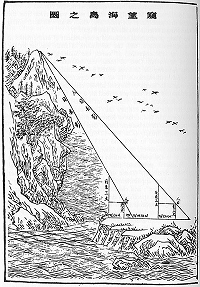
《海島算經(jīng)》示意圖

　　古人很早就知道，把角尺直立在物體的水平位置上，對準要測量的物體，使物體的最高點，與角尺兩邊上的兩點連成一線，利用相似直角三角形對應邊成比例的性質，就可以把物體的高度計算出來了。數(shù)學家劉徽就系統(tǒng)地總結并舉例解釋了這種方法，撰寫成專門的一卷《重差》，附在古代數(shù)學名著《九章算術》之后。因為它的第一題是關于測量海島的高和遠的問題，所以《重差》在后面也被叫做《海島算經(jīng)》。

　　古人對于世界的探索思想也是無窮無盡的，那太陽究竟有多高呢？有的天文學家認為天圓地方，于是他們就將這種方法應用到了測量太陽高度上。地球是一望無際的平地，太陽的高度是可以在特定的時間和地點測量計算的。他們用一根八尺長的標桿，選定夏至這一天，在南北相隔一千里的兩個地方分別測量出太陽影子的長度，再根據(jù)相似直角三角形對應邊成比例的性質，得出太陽離地面的高度。但是，因為假設地面是平的，不符合實際情況，所以得出錯誤的結果。不過，“重差術”這種數(shù)學方法是正確的。

　　《海島算經(jīng)》（《重差》）是中國最早的一部測量數(shù)學著作，為地圖學提供了數(shù)學基礎，標志著中國古代測量數(shù)學的偉大成就。

　　1500年前的“雞兔同籠”問題

“雞兔同籠”問題示意圖

　　大多數(shù)人聽到雞兔同籠就想起被數(shù)學支配的恐懼，不過這個問題可是早在1500年前就被提出和記載在《孫子算經(jīng)》里了，被稱作古代著名的三大趣題之一。

　　原題是：“今有雉兔同籠，上有三十五頭，下有九十四足，問雉兔各幾何？”意思是：現(xiàn)在有若干只雞和兔子被關在一個籠子里，有35個頭和94只腳。問籠中各有多少只雞和兔。

　　孫子的解法是：砍去其中一半的腳，那么現(xiàn)在就有47只腳，雞變成了“獨腳雞”，兔變成了“雙腳兔”，每只雞的頭數(shù)與腳數(shù)之比變?yōu)?：1，每只兔的頭數(shù)與腳數(shù)之比變?yōu)?：2。由此可知，有一只“雙腳兔”，腳的數(shù)量就會比頭的數(shù)目多1。所以，“獨腳雞”和“雙腳兔”的腳的數(shù)量與他們的頭的數(shù)量之差，就是只數(shù)，即兔的數(shù)量是：47－35=12（只）；雞的數(shù)量就是：35－12=23（只）。這一思路新穎而奇特，其“砍足法”也令古今中外數(shù)學家贊嘆不已。

　　看了那么多古代數(shù)學成就，不得不稱贊古人的智慧。古代的工具、技術都遠沒有現(xiàn)在發(fā)達，祖先們在生活中發(fā)現(xiàn)和思考，創(chuàng)造出一個又一個精妙的方法，用不懈的探索精神將中華數(shù)學推向一個又一個高峰。

　　中國古代數(shù)學成就不勝枚舉，寥寥幾句只是描摹輪廓。都說“長江后浪拍前浪”，當代年輕人要善于思考，站在巨人的肩膀上繼續(xù)努力，因為智慧是不會枯竭的，思想和思想相碰，就會迸發(fā)無數(shù)火花。

來源：文藝星青年　責編：黃雪萊(實習生)、丁濤